Einleitung
Mittlerweile stehen dem Heimbrauumfeld eine breite Auswahl von Instrumenten mit verschiedenen Messprinzipien zur Verfügung, die es ermöglichen, den Alkoholgehalt eines selbst gebrauten Biers abzuschätzen oder den Gärverlauf zu beobachten. Das ist neben der klassischen Bierspindel unter anderem das Handrefraktometer. Die Refraktometrie ist kein Neuling im Bereich der Bieranalyse. Versuche, auf Basis dieses Messprinzips den Alkoholgehalt zu bestimmen, reichen bis in das Jahr 1843 zurück (Gamer, 1959, S. 102).
Auch wenn Refraktometer den Ruf besitzen, weniger genaue Messergebnisse zu liefern als andere labortechnische Instrumente, liegen deren Vorteile klar auf der Hand: kurze Messzeiten bei geringem Probevolumen und überschaubarer Bedienungskomplexität. Im Gegensatz zu den bei der Bierspindel üblichen 100 Millilitern pro Probe werden nur wenig Milliliter benötigt, die sich dementsprechend auch schneller nach dem Hopfenkochen auf Messtempertur abkühlen lassen. (Bettner & Meredith, 1969, S. 171 f.; Terrill, 2011)
Wie nun Messungen mit einem Refraktometer während des Brau- und Gärprozesses durchzuführen sind und sich darauf basierend der Alkoholgehalt als Näherungswert berechnen lässt, wird im Rahmen dieses Artikels erörtert.
Messprinzip und Gerätetypen
Wenn Licht auf eine Grenzfläche zwischen unterschiedlich optisch dichten Medien (verschiedene Brechungsindexe) trifft, kommt es zur Lichtbrechung und Reflexion. Dieser physikalische Effekt wird in einem Refraktometer als Brechungsindex quantifiziert. Maßgeblich zur Messwertbestimmung ist der materialabhängige kritische Einfallswinkel, ab dem keine Brechung mehr stattfindet. Der Brechungsindex nD ist als Verhältnis zwischen der Geschwindigkeit von Licht im Vakuum und einem Medium definiert. Je höher die optische Dichte ist, desto größer ist auch der Brechungsindex. (A.KRÜSS Optronic GmbH, 2021; Bonham, 2001, S. 43; Gamer, 1959, S. 102 f.)
Refraktion ist temperaturabhängig. Messungen sind daher je nach Anwendungsgebiet bei einer festgelegten Temperatur durchzuführen. Das ist im Normalfall 20 °C. Selbst kostengünstige Handrefraktometer besitzen deshalb einen Kompensationsmechanismus (Automatical Temperature Compensation, ATC) in Form eines Bimetallstreifens. Dieser verschiebt je nach Temperatureinwirkung zur Korrektur selbstständig die Messskala des Geräts. Hierbei ist zu beachten, dass diese Form der ATC nur für den kalibrierten Probentyp des Geräts ausgelegt ist. (DePalma, 2017; Distillique, 2020; Gossett, 2012c; Terrill, 2013, S. 50)
Der Brechungsindex ist mitunter keine geeignete Messgröße für alle technischen Prozesse. Deshalb wird er je nach Anwendungsgebiet und Probe auf die gewünschte Messgröße kalibriert. Zur Messung der relativen Dichte von Saccharose/Wasser-Lösungen im Bereich der Wein- und Saftherstellung ist diese zum Beispiel Grad Brix (°Bx), wobei ein °Bx einem Gramm Saccharose auf 99 Gramm Wasser entspricht. (Bonham, 2001, S. 43; Terrill, 2013, S. 50)
In den Shops für Heimbraubedarf werden im Wesentlichen Refraktometer in zwei verschiedenen Bauformen angeboten: analoge Handgeräte und kompakte digitale Tischgeräte, wie das für die Weinherstellung gedachte Milwaukee MA885 (Abb. 1, Tab. 1). Beide Bauformen setzen Prismen zur Lichtbrechung ein. Handrefraktometer funktionieren nach dem Durchlichtprinzip. Vereinfacht dargestellt scheint dabei Licht von einer externen Quelle durch die Probe, wird über Prismen gebrochen und durch weitere optische Komponenten und eine Skala bis hin zu einem Okular geleitet. Unterschiedliche kritische Winkel erzeugen dabei eine andere Teilung des Sichtfelds, anhand der der Messwert abgelesen werden kann (Abb. 2). Im Unterschied dazu besitzen digitale Refraktometer eine interne Lichtquelle und erfassen die Messung über einen CCD-Sensor. Das Licht muss dabei für die Brechung die Probe nicht durchqueren. (A.KRÜSS Optronic GmbH, 2021; Gamer, 1959, S. 102 f.; Terrill, 2013, S. 50)

Abb. 1: Typische Refraktometer im Heimbraubereich (Ascher, 2021)

Abb. 2: Durchsicht durch ein Handrefraktometer (Ascher, 2021)
| Parameter | Handrefraktometer | Milwaukee MA885 |
|---|---|---|
| Preis [€] | 40 | 185 |
| Messbereich [°Bx] | 0–32 | 0–50 |
| Auflösung [°Bx] | 0,2 | 0,1 |
| Genauigkeit [°Bx] | 0,2 | 0,1 |
| ATC [°C] | 10–30 | 10–40 |
| Maßeinheiten | °Bx, SG | °Bx, °Oe, °KWM |
| Kalibrierschein | nein | ja |
Exkurs Bierspindel
Für Vergleichsmessungen zu einem Refraktometer oder zur Kalibrierung des refraktometerspezifischen Würze-Korrekturfaktors (Wort Correction Factor, WCF) wird im Heimbraubereich meist eine Bierspindel eingesetzt. Darüber hinaus decken sich die Berechnungswege für den Alkoholgehalt und weiterer Kennzahlen für beide Messgeräte, da mit einem Refraktometer erfasste Messwerte üblicherweise in Spindelwerte umgerechnet werden.
Eine Bierspindel (auch Saccharometer) ist ein auf Massenanteil kalibriertes Aräometer. Mit einem Aräometer lässt sich die spezifische Dichte (Specific Gravity, SG) einer Flüssigkeit auf Basis des Archimedischen Prinzips messen. Das heißt, dass ein in Flüssigkeit eingetauchter Körper Auftrieb in dem Maß der Gewichtskraft der dabei verdrängten Flüssigkeit erfährt. Je geringer die Dichte einer Flüssigkeit dabei ist, desto weiter sinkt ein Körper ein. Hierbei ist zu beachten, dass die Dichte temperaturabhängig ist. Daher wird für die spezifische Dichte eine Referenztemperatur angegeben. Für die in diesem Artikel beschriebenen Angaben und Berechnungen entspricht sie 20 °C. Bei Abweichungen von dieser Referenz ist eine Messwertkorrektur durchzuführen. Messwerte müssen von der Skala je nach Aräometer über oder unter dem gebildeten Flüssigkeitsmeniskus abgelesen werden. (Kunze, 2004, S. 324 ff.; Narziss & Back, 2009, S. 647 f.; Spedding, 2016, S. 131)
Für verschiedene Abschnitte im Brauprozess existieren spezialisierte Spindelausführungen. Das sind die universelle, auf 20 °C kalibrierte Sudhausspindel, die zum Läutern auf 70 °C kalibrierte Läuterspindel mit weniger feiner Graduierung (rote Kennzeichnung) und die auf die Gärung und Kellertemperaturen ausgelegte Keller-/Endvergärungsspindel (grüne Kennzeichnung) (Brückelmeier, 2018, S. 381 ff.).
In den USA führen Heimbrauer:innen Spindelmessungen zumeist mit einem Hydrometer durch, um die relative Dichte von Würze in Bezug auf Wasser festzustellen. Die Skala einer Bierspindel ist hingegen auf Grad Plato kalibriert. Grad Plato (°P) ist das Maß für die vor der Gärung gemessene Stammwürze eines Bieres (Original Extract, OE), wobei ein °P einem Gramm Extrakt auf 100 Gramm Bier entspricht. Mit Extrakt sind vor allem die Bestandteile gemeint, die während des Maischeprozesses aus dem Malz gelöst werden. Die Umrechnung zwischen Massenanteil in °P und der Massendichte erfolgt auf Basis der Plato Tabellen über die Lincoln Gleichungen (Gl. 1, Gl. 2) oder vergleichbaren Näherungsverfahren. (Kunze, 2004, S. 648; Spedding, 2016, S. 126, 140 f.)
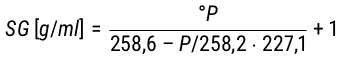
Gl. 1
Gl. 2
Während und nach einer Gärung kann der scheinbare Restextrakt (Apparent Extract, AE) gemessen werden. Scheinbar deshalb, weil der während der Gärung gebildete Alkohol die Dichte der Flüssigkeit verändert und somit den Messwert verfälscht. Der wirkliche Restextrakt (Real Extract, RE) entspricht nämlich einem höheren Betrag. Das ebenfalls in Gärproben oder in Jungbieren enthaltene CO2 hat ebenfalls einen Einfluss auf den Messwert. Es erhöht diesen um circa 0,3 g/100g. (Novotný, 2017b, S. 53; Spedding, 2016, S. 125)
Für genaue Messergebnisse sollten Spindeln mit einem möglichst geringen Messbereich eingesetzt werden. In Heimbraushops sind zum Beispiel Saccharometer mit einem Messbereich von 7 °P und einer Graduierung von 0,1 °P erhältlich. Der geringe Messbereich ermöglicht eine einfachere Ablesung und eine feinere Graduierung. Für Hydrometer empfiehlt die Mitteleuropäische Brautechnische Analysenkommission (MEBAK) Messgeräte, die der DIN 12791-1 Norm entsprechen. Darüber hinaus sollten folgende Vorgehensweisen eingehalten werden (MEBAK, 2013, S. 143; Narziss & Back, 2009, S. 647 f.; Wolf, 2015):
- Eine Probe ist auf die ungefähre Temperatur des Messgeräts abzukühlen oder zu erwärmen. Um eine Verdunstung zu vermeiden, ist die Probe abzudecken.
- Proben sind vor der Messung gut zu durchmischen.
- Während oder nach einer Gärung entnommene Proben sind durch mehrmaliges Schütteln zu entgasen. Am Messgerät anhaftende Gasblasen lassen sich durch schnelles Eintauchen in und Herausziehen aus der zu messenden Probe entfernen.
- Messgerät und Messgefäß sollten trocken und rein sein und waagrecht stehen.
- Das Messgefäß sollte die Bierspindel oder das Hydrometer ohne großen Spielraum aufnehmen können.
- Beim Ablesen des Messwerts ist die gegebenenfalls aufgedruckte Leserichtung der Spindel zu berücksichtigen und danach die Temperaturkorrektur auf 20 °C durchzuführen.
Im Jahr 2017 wurde ein Ringversuch zur Feststellung der „Gesamtgüte“ der von Heimbrauer:innen eingesetzten Bierspindeln und Refraktometern im Vergleich zu labortechnischen Geräten des Unternehmens Anton Paar anhand von zwei Referenzproben durchgeführt. Dabei hat sich gezeigt, dass mit Präzisionsspindeln erhobene Messwerte nur geringe Abweichungen zu den Ergebnissen des Laborgeräts aufweisen. Im Durchschnitt und im Extremfall erzeugen kostengünstige Refraktometer jedoch geringere Abweichungen als kostengünstige Bierspindeln. Dabei ist jedoch zu beachten, dass die bei Refraktometern notwendige Umrechnung des Messwerts eine zusätzliche Abweichung von bis zu 0,42 g/100g verursachen kann. (Sauseng et al., 2017)
Messung
Vor einer Messung sollte der Probenaufnahmebereich eines Refraktometers und die zum Transfer der Probe eingesetzte Pipetten mit destilliertem Wasser gereinigt werden, um eine Messwertverfälschung durch Rückstände vorheriger Proben zu verhindern. Neben Kontaminierungen ist die Temperatureinwirkung einer der häufigsten Quellen für Messfehler. Das eingesetzte Refraktometer sollte daher auf Raumtemperatur erwärmt sein. Danach ist eine Einpunkt-Kalibrierung durchzuführen. (DePalma, 2017)
Proben bedürfen einer Aufbereitung. Darin enthaltene Schwebestoffe und Gase sind zu entfernen. Das heißt, dass während der Gärung entnommene Proben längere Zeit stehen gelassen werden müssen, bis ein Großteil der darin enthaltenen Hefe sedimentiert ist. Zur Entfernung von CO 2 kann die Probe innerhalb eines Behälters mehrmals geschüttelt werden. Inzwischen ist der Behälter kurz zu öffnen, damit das Gas entweichen kann. Heiße Würze sollte nicht direkt auf ein Refraktometer aufgetragen werden, da es hierbei zu Verdampfungen kommt und somit zu einer Konzentrationsänderung. Proben sind daher, bis diese die Raumtemperatur angenommen haben, in einem abgedeckten Behälter aufzubewahren. (Gamer, 1959, S. 105; MEBAK, 2013, S. 140 f., 150 f.; Terrill, 2013, S. 51 f.)
Für die eigentliche Messung sind mittels Pipette einige Tropfen der Probe auf den Probenaufnahmebereich aufzutragen (Abb. 3). Beim Handrefraktometer ist danach die Abdeckung zu schließen und dann das Messgerät zum Ablesen des Messwerts gegen eine Lichtquelle zu richten. Der Betrag des gemessenen Werts wird durch die Trennlinie zwischen farblichem und farblosem Bereich signalisiert (Abb. 2). Ist die Trennlinie verschwommen, befinden sich mitunter Schwebestoffe in der Probe. Beim MA885 wird die Messung nach dem Einschalten durch Drücken der Taste „Read“ ausgelöst. Der Messwert ist danach vom Display abzulesen. Bei digitalen Refraktometern ist zu beachten, dass durch externe Lichtquellen verursachte Interferenzen die Messung beeinflussen können. (Gossett, 2012a; Terrill, 2013, S. 50 ff.)

Abb. 3: Durchführung einer Messung (Ascher, 2021)
Kalibrierung und Justierung
Um sicherzustellen, dass ein Messgerät dauerhaft genaue Messergebnisse liefert, ist in regelmäßigen Abständen eine Kalibrierung durchzuführen, das heißt, den mit dem Messgerät erfassten Messwert mit einer bekannten Referenz (rückführbarer Kalibrierstandard) zu vergleichen und die Abweichung festzustellen. Das sind bei Refraktometern zum Beispiel wässrige Zuckerlösungen mit einem definierten Zuckergehalt. Wird eine unerwünschte Abweichung festgestellt, kann sie durch Justierung des betroffenen Messgeräts ausgeglichen werden.
Eine Kalibrierung ist je nach Anzahl der gemessenen Referenzen eine Einpunkt-, Zweipunkt- oder Mehrpunkt-Kalibrierung. Bei der Einpunkt-Kalibrierung wird im Wesentlichen ein definierter Nullpunkt gesetzt. Die Erfassung von mehreren Messpunkten erlaubt die Korrektur von linearen oder nicht linearen Abweichungen über den Messbereich. Ab zwei Messpunkten kann eine Ausgleichsgerade bestimmt und ab drei Messpunkten eine Polynomfunktion eingepasst werden. (Earl, 2015)
Vor jeder Messserie empfiehlt sich die Durchführung einer Einpunkt Kalibrierung bei Raumtemperatur mit destilliertem Wasser. Ein Refraktometer sollte dabei die Raumtemperatur angenommen haben und gereinigt sein. Zur Kalibrierung ist eine Messung mit destilliertem Wasser als Probe durchzuführen. Der abgelesene Messwert muss 0 °Bx betragen (Abb. 2). Wird eine Abweichung festgestellt, kann ein Handrefraktometer durch Drehen an der Einstellschraube justiert werden (Abb. 4), bis die Anzeige 0 °Bx beträgt. Beim MA885 erfolgt die Justierung durch Drücken der Taste „Zero“. (Bonham, 2001, S. 44; DePalma, 2017; Terrill, 2013, S. 50 f.)

Abb. 4: Justierung eines Handrefraktometers (Ascher, 2021)
Messgeräte sollten nach der Herstellung einer ausreichenden Qualitätssicherung unterzogen werden. Bei günstigen Handrefraktometern muss dies nicht zwangsweise der Fall sein (Troester, 2012). Zur Feststellung, ob die integrierte Messskala eine zufriedenstellende Abdeckung des Messbereichs bietet, lässt sich eine Zweipunkt-Kalibrierung durchführen (Earl, 2015; Terrill, 2013, S. 50 f.). Da der Preis eines Kalibrierstandards im Normalfall deutlich über den Anschaffungskosten des Messgeräts liegt, kann stattdessen eine Referenzlösung mit Haushaltszucker, destilliertem Wasser und einer Feinwaage hergestellt werden. Zuerst ist beim betroffenen Refraktometer, wie zuvor beschrieben, der Nullpunkt zu kalibrieren und justieren. Danach ist eine Referenzlösung für den oberen Bereich der Messskala herzustellen. Eine Lösung für 32 °Bx entspricht dabei 32 g Zucker auf 68 g Wasser. Die festgestellte Abweichung lässt sich nicht justieren, aber durch Aufstellen einer Geradengleichung korrigieren.
Würze-Korrekturfaktor und Stammwürze
Während sich die Einheit °Bx auf den Zuckeranteil in wässrigen Saccharoselösungen bezieht, beschreibt °P den Extraktgehalt. Ein auf °Bx kalibriertes Refraktometer sollte daher bei gleicher Stammwürze einen höheren Messwert anzeigen als eine Bierspindel. Der Grund dafür ist, dass Extrakt neben verschiedenen Zuckern noch weitere Bestandteile wie Säuren, Salze, Proteine und Hopfenöle enthält, die sich auf den Brechungsindex auswirken. Messwerte müssen dementsprechend durch einen Korrekturfaktor (Wort Correction Factor, WCF) angepasst werden. Zur Ermittlung der Stammwürze in °P ist daher der Messwert des Refraktometers der Stammwürze (Ri) gemäß Gl. 3 durch den WCF zu dividieren. (Bonham, 2001, S. 43; Brew Science Homebrewing Blog, 2010; Roberts & Stewart, 1950, S. 119; Terrill, 2013, S. 51)
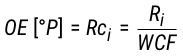
Gl. 3
Der WCF ist stark von der Würzezusammensetzung und zum Teil auch vom eingesetzten Messgerät abhängig und sollte deshalb pro unterschiedlicher Schüttung mithilfe einer Extraktmessung durch ein anderes Messgerät gemäß Gl. 4 bestimmt werden. Der etablierte Durchschnittswert für den WCF entspricht 1,04 und bezieht sich auf die Messdifferenz zu einem Pyknometer. (Bonham, 2001, S. 44; Roberts & Stewart, 1950, S. 119; Terrill, 2013, S. 51)
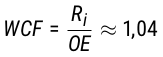
Gl. 4
Korrelationsmodelle und scheinbarer Restextrakt
Das während der Gärung gebildete Ethanol verfälscht nicht nur die Extraktmessung mit der Bierspindel, sondern beeinflusst auch den Brechungsindex. Es besteht daher die Notwendigkeit, einen Refraktometermesswert für die Berechnung des Alkoholgehalts in eine andere Messgröße zu transformieren. Die entsprechende Messgröße ist im Normalfall der scheinbare Restextrakt, so wie er mit einer Bierspindel gemessen würde. Die Umrechnung erfolgt durch eine Korrelationsfunktion. Insgesamt wurden mindestens fünf Korrelationsmodelle im Heimbrauumfeld für diesen Zweck veröffentlicht, die ihre jeweiligen Stärken und Schwächen besitzen. Ein grundlegendes Problem bei der Entwicklung eines solchen Modells ist, dass verschiedene Zusammensetzungen einer vergorenen Probe den gleichen Brechungsindex aufweisen können. (Distillique, 2020; Terrill, 2010a; Terrill, 2010b)
Zur Berechnung der folgenden Korrellationsfunktionen ist eine Probe der Anstellwürze vor der Gärung (Ri) und eine während oder nach der Gärung entnommene Probe (Rf) mit einem Refraktometer zu messen. Je nach Funktion sind unveränderte (Ri, Rf) oder um den Würze-Korrekturfaktor angepasste Messwerte (Rci , Rcf) einzusetzen.
Gardner
Das lineare Gardner Modell zu Berechnung des scheinbaren Restextrakts (Gl. 5) wurde im Jahr 2000 in der Zeitschrift „The New Brewer“ veröffentlicht und von existierenden Gleichungen abgeleitet. Bonham beschreibt dieses Modell als ausreichend genau für die private Anwendung, weißt aber darauf hin, dass bereits bessere Näherungsverfahren zu diesem Zeitpunkt existiert hätten. Neben der Gleichung zur Bestimmung des scheinbaren Restextrakts hat Gardner auch eine Gleichung zur Bestimmung des Alkoholgehalts in Gewichtsprozent (Alcohol by Weight, ABW, Gl. 6) aufgestellt. (Bonham, 2001, S. 44)
Gl. 5
Gl. 6
Im Heimbraubereich scheint das Gardner Modell keine große Verbreitung erfahren zu haben.
Bonham
Das von Bonham im Jahr 2001 im Zymurgy Magazin der American Homebrewers Association veröffentlichte Korrelationsmodell ist auch als Standardformel bekannt. Als Grundlage dienten bereits existierende Gleichungen, die an die üblichen Messgrößen in der amerikanischen Heimbrauszene angepasst wurden. Bis zur Ablösung durch die Terrill Formel ab dem Jahr 2011 war dieses Modell weit verbreitet. Heute wird es noch vereinzelt, wie zum Beispiel von „Maische, Malz und Mehr“, für Messungen während der Gärung empfohlen. (Bonham, 2001, S. 44; Terrill, 2010a)
Das Bonham Modell besteht aus einer Gleichung zur Bestimmung der spezifischen Dichte eines vergorenen Bieres (Gl. 7) und einer Gleichung zur Bestimmung des Alkoholgehalts in Volumenprozent (Alcohol by Volume, ABV, Gl. 8).
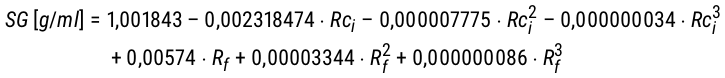
Gl. 7
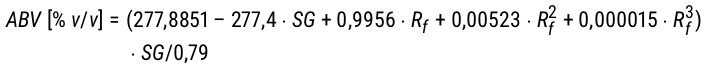
Gl. 8
Terrill
Bei Vergleichsmessungen zwischen einem Hydrometer und einem Handrefraktometer in Verbindung mit der Bonham Gleichung hat Terrill im Jahr 2010 eine mittlere Abweichung der Messwerte von 1,3 g/100g festgestellt und darauf hin mit der Entwicklung eines eigenen Korrelationsmodells begonnen, welches er in linearer (Gl. 9) und vereinfachter kubischer Form (Gl. 10) veröffentlicht hat. (Terrill, 2010a)
Gl. 9

Gl. 10
Insgesamt dienten Vergleichsmessungen von 12 Bieren mit Stammwürzen von 9 bis 24 °P, scheinbaren Restextrakten von 1,8 bis 5,6 g/100g und scheinbaren Vergärungsgraden von 73 bis 91 % als ursprüngliche Datenbasis. Messungen mit geringeren Vergärungsgraden wurden ausgeschlossen, da diese die Genauigkeit des Modells verschlechtert hätten. (Terrill, 2010a, 2010b, 2011)
Tab. 2 zeigt den von Terrill veröffentlichten Vergleich zwischen dem Modell von Bonham und seinem eigenen. Bei endvergorenen Proben erzeugt das Bonham Modell höhere Abweichungen. Hierbei ist allerdings zu beachten, dass Terrill die ursprüngliche Quelle des Bonham Modells nicht bekannt war und er deshalb fälschlicherweise auch den Messwert nach der Gärung um den Würze-Korrekturfaktor angepasst hat. Dieser Fehler soll sich aber nicht signifikant auf das Vergleichsergebnis auswirken. (Terrill, 2010a, 2010b, 2011)
| Statistik | BO | TK | TL |
|---|---|---|---|
| Max. Abw. [g/100g] | -2,1 | 1,2 | 1,0 |
| Mittlere Abw. [g/100g] | -0,4 | 0,2 | 0,0 |
| Standardabw. [g/100g] | 0,6 | 0,3 | 0,4 |
| Abw. < 0,25 g/100g [%] | 18 | 56 | 63 |
| Abw. < 0,50 g/100g [%] | 41 | 85 | 84 |
| Abw. < 1,00 g/100g [%] | 90 | 97 | 99 |
Gossett
Von den zuvor beschriebenen Korrelationsmodellen wird ein indirekter Messwert in einen anderen transformiert. Gossett war unzufrieden mit diesem Vorgehen und hat im Jahr 2012 daher ein stöchiometrisches Modell (Gl. 11, Gl. 12) entwickelt, welches direkt den Alkohol in Gewichtsprozent auf Basis von Refraktometermesswerten berechnet. Er hat hierzu die Auswirkungen der Ethanolkonzentration auf die Messwerte eines Refraktometers analysiert. Ein Gewichtsprozent verfälscht diesen bei 20 °C um 0,445 °Bx. (Gossett, 2012a, 2012b, 2012c)
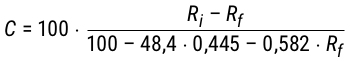
Gl 11.
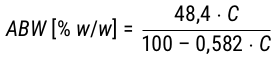
Gl 12.
Mit dem Gossett Modell lässt sich direkt keine spezifische Dichte zur Berechnung von Gl. 20 bestimmen. Gossett wendet hierzu Gl. 7 an. Durch Umformung von Gl. 18 und Gl. 19 ist aber eine Berechnung aus dem durch Gl. 12 erhaltenen Alkoholgehalt möglich.
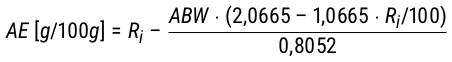
Gl. 13
Novotný
Um das Jahr 2017 hat sich Novotný mit bestehenden Berechnungsvorschriften im Heimbraubereich beschäftigt und nach Verbesserungsmöglichkeiten gesucht. Darunter auch die Terrill Formel, da diese bekannt dafür ist, während der Anfangszeit einer Gärung hohe Abweichungen zu verursachen. Basierend auf einer durch die Brauerei Budweis beauftragte Forschungsarbeit zur Bewertung von Refraktometern (ŠAVEL et al., 2009) als Messmittel hat Novotný eine lineare (Gl. 14) und eine quadratische (Gl. 15) Gleichung zur Berechnung der spezifischen Dichte veröffentlicht. Darüber hinaus auch noch Formeln zur Berechnung des wirklichen Restextrakts (Gl. 16) und des Alkoholgehalts in Gewichtsprozent (Gl. 17). (Novotný, 2017a, 2017b)
Gl. 14

Gl. 15
Gl. 16
Gl. 17
Das Novotný Modell wurde während der Gärung an drei Testsuden mit jeweils 11,6 °P, 17 °P und 20 °P Stammwürze und an den Budweiser Ergebnissen verifiziert. Laut den erhobenen Daten liefert das Terrill Modell im Vergleich während der ersten Tage der Gärung höhere Abweichungen und auch eine geringfügig höhere Endabweichung. (Novotný, 2017a; Novotný, 2017b)
Terrill & Novotný
Von den vorgestellten Korrelationsmodellen scheinen nur die Modelle von Bonham, Terrill und Novotný eine weitere Verbreitung im Heimbraubereich erfahren zu haben, wobei das Modell von Terrill selbst heute nach wie vor als „Quasi Standard“ gilt. Neuere Braurechner, wie zum Beispiel „Brewfather“ oder „Brewer’s Friend“, implementieren jedoch das Novotný Modell. Dementsprechend findet sich auf Diskussionsplattformen öfters die Fragestellung, ob nun entweder die Terrill oder die Novotný Formel herangezogen werden soll. Im Rahmen einer solchen Diskussion im Jahr 2020 hat Terrill basierend auf seinem aus mittlerweile 40 Messungen bestehendem Datensatz einen Vergleich (Tab. 3) hierzu veröffentlicht. Nach Ansicht von Terrill ist sein Modell auf Genauigkeit bei endvergorenen Proben optimiert, das Novotný Modell hingegen auf den gesamten Messbereich eines Gärverlaufs. Darüber hinaus wurde während dieser Diskussion auf Basis von Terrills Datensatz ebenfalls festgestellt, dass das Terrill Modell bei einem scheinbaren Restextrakt kleiner als 3,8 g/100g (1,014 g/ml) geringere Abweichungen erzeugt, bei einem höheren jedoch das Modell von Novotný. Um geringere Abweichungen zu erzielen, wäre es daher denkbar, mit beiden Modellen eine Vorabschätzung des scheinbaren Restextrakts durchzuführen und anhand dieser Abschätzung das besser geeignete Modell zu wählen. Für den folgenden Vergleich wird der Mittelwert beider Korrelationen herangezogen. („Sean Terrill’s website issues“, 2020)
| Statistik | NL | NQ | TK | TL |
|---|---|---|---|---|
| Mittlere Abw. [g/100g] | -0,4 | -0,5 | 0,0 | -0,1 |
| Standardabw. [g/100g] | 0,5 | 0,5 | 0,3 | 0,4 |
Modellvergleich
Vereinfacht dargestellt erzeugt das Terrill Modell eine sehr geringe Abweichung nach, aber nicht während der Gärung. Bonham und Novotný liefern über den gesamten Gärverlauf eine vertretbare Korrelation, wobei Novotný bei einem scheinbaren Restextrakt größer als 3,7 g/100g geringere Abweichungen erzeugt als Terrill. Für die anderen zwei Modelle liegen keine öffentlichen Vergleiche vor. Es wäre daher interessant, alle Modelle an einer Messreihe zu evaluieren. Datensätze mit einigen Messwerten wurden im HomebrewTalk Forum, von einem vom hobbybrauer.de Forum initiierten Gemeinschaftsexperiment und von Novotný veröffentlicht (Novotný, 2017a; „Refractometers and final gravity“, 2019; Wolf, 2015).
Abb. 5 und Tab. 4 zeigen die Auswertung der von Novotný veröffentlichten Messdaten zu einem Gärverlauf bei 17 °P Stammwürze (WCF = 1,0). Alle Modelle, außer dem Terrill Modell, erzeugen vertretbare Abweichungen über den gesamten Gärverlauf. Die geringsten Endabweichungen sind beim Novotný und Terrill Modell zu finden. Das Gossett Modell korreliert den Alkoholgehalt. Der scheinbare Restextrakt wurde deshalb durch Gl. 13 berechnet. Ein Vergleich ist daher nur bedingt aussagekräftig.
| Statistik | BO | GA | GO | NL | NQ | TK | TL | TN |
|---|---|---|---|---|---|---|---|---|
| Endabw. [g/100g] | -0,6 | -0,5 | -0,5 | -0,0 | -0,1 | 0,2 | 0,3 | -0,0 |
| Max. Abw. [g/100g] | -0,8 | -1,1 | -0,6 | -0,8 | -0,6 | 9,0 | -5,9 | -0,8 |
| Mittlere Abw. [g/100g] | -0,5 | -0,7 | -0,3 | -0,2 | -0,3 | 1,3 | -1,8 | -0,2 |
| Standardabw. [g/100g] | 0,1 | 0,2 | 0,2 | 0,2 | 0,2 | 3,2 | 2,1 | 0,2 |
| Abw. < 0,25 g/100g [%] | 0,0 | 0,0 | 33,3 | 66,7 | 55,6 | 33,3 | 22,2 | 66,7 |
| Abw. < 0,50 g/100g [%] | 22,2 | 22,2 | 88,9 | 88,9 | 88,9 | 55,6 | 33,3 | 88,9 |
| Abw. < 1,00 g/100g [%] | 100,0 | 88,9 | 100,0 | 100,0 | 100,0 | 77,8 | 44,4 | 100,0 |
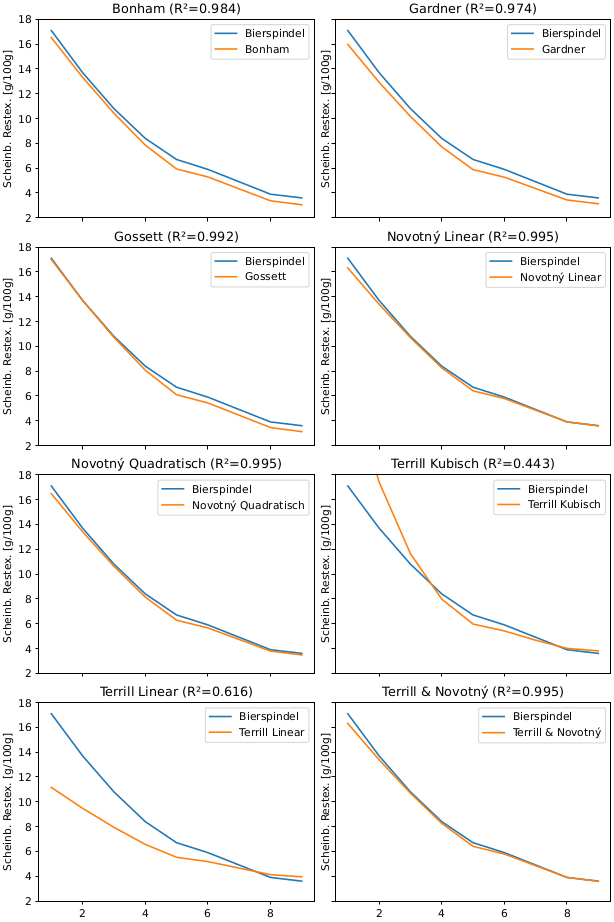
Abb. 5: Scheinbarer Restextrakt bei Gärverlauf (Ascher, 2021)
Der Vergleich der Messdaten endvergorener Proben in Abb. 6 und Tab. 5 erfolgt anhand aller genannten Datensätze, wobei von Novotný nur der letzte Messwert zu übernehmen ist. Für die Messdaten des HomebrewTalk Forums lässt sich ein durchschnittlicher Würze-Korrekturfaktor von WCF = 0,99 berechnen. Die Umrechnung von spezifischer Dichte zu scheinbarem Restextrakt erfolgt über Gl. 2. Für die Messdaten des hobbybrauer.de Forums wird WCF = 1,03 angenommen. Ohne eine weitere Vorverarbeitung der Messdaten erzeugen die meisten Korrelationsmodelle eine hohe maximale Abweichung (bis zu 4,7 g/100g). Es ist unklar, ob es sich dabei um Messfehler handelt. Zur Behandlung solcher statistischer Ausreißer wurde eine Höchstgrenze für Abweichungen von 1,88 g/100g basierend auf dem dreifachen Interquartilsabstand der maximalen absoluten Abweichungen definiert. Diese Schranke entfernt 4 von 47 Messungen. Abb. 6 zeigt die Verteilung der Abweichungen nach der Filterung. Gemäß der Statistik von Tab. 5 verursacht der kombinierte Terill & Novotný Ansatz die geringsten Abweichungen. Insgesamt ist aber anzumerken, dass eine geringfügige Änderung des WCF die Ergebnisse zugunsten anderer Modelle verschiebt.
| Statistik | BO | GA | GO | NL | NQ | TK | TL | TN |
|---|---|---|---|---|---|---|---|---|
| Max. Abw. [g/100g] | -1,8 | -1,8 | -1,7 | -1,4 | -1,5 | 1,7 | 1,3 | 1,3 |
| Mittlere Abw. [g/100g] | -0,4 | -0,5 | -0,4 | -0,2 | -0,3 | 0,2 | 0,0 | 0,1 |
| Standardabw. [g/100g] | 0,4 | 0,4 | 0,4 | 0,4 | 0,4 | 0,5 | 0,5 | 0,4 |
| Abw. < 0,25 g/100g [%] | 32,6 | 27,9 | 39,5 | 58,1 | 39,5 | 46,5 | 46,5 | 65,1 |
| Abw. < 0,50 g/100g [%] | 62,8 | 65,1 | 69,8 | 81,4 | 76,7 | 74,4 | 72,1 | 83,7 |
| Abw. < 1,00 g/100g [%] | 90,7 | 90,7 | 88,4 | 97,7 | 93,0 | 95,3 | 95,3 | 97,7 |
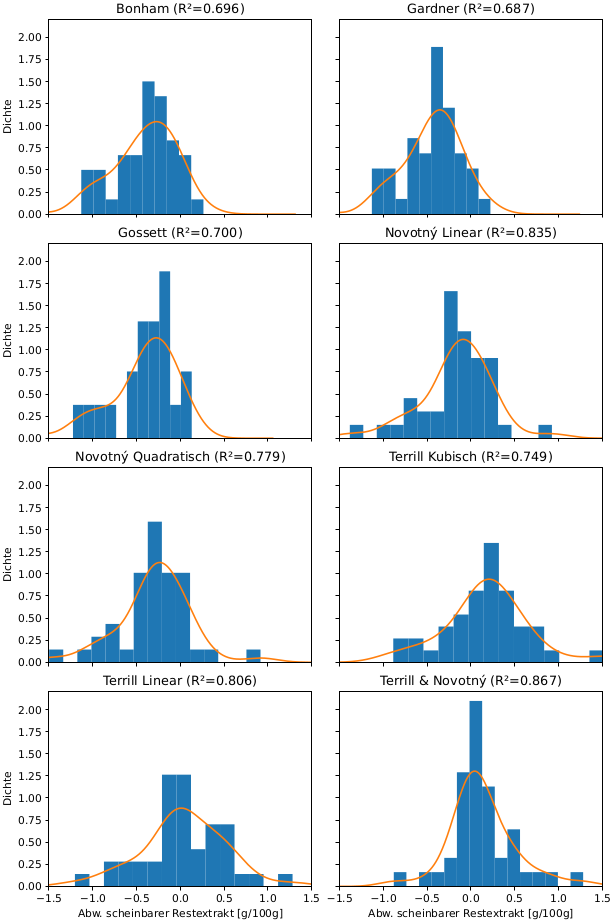
Abb. 6: Histogramme der Abweichungen des scheinbaren Restextrakts bei endvergorener Probe
(Ascher, 2021)
Bestimmung des Alkoholgehalts und weiterer Kennzahlen
Der durch die Balling Formel formulierte Zusammenhang zwischen scheinbarem Restextrakt, wirklichem Restextrakt, Stammwürze und Alkoholgehalt kann dazu verwendete werden, um aus der Menge des während einer Gärung durch die Hefe konsumierten Extrakts den daraus resultierenden Alkoholgehalt ohne aufwendigere analytischer Verfahren als Näherungswert zu berechnen. Dafür muss eine Messung der Stammwürze vor der Gärung und eine Messung des scheinbaren Restextrakts während oder nach der Gärung durchgeführt werden. (MEBAK, 2013, S. 139 f.; Spedding, 2016, S. 137 ff.)
Bei Messungen mit einem Refraktometer ist dabei die gemessene Stammwürze durch den Würze-Korrekturfaktor und der gemessene scheinbare Restextrakt durch eine Korrelationsfunktion zu korrigieren. Für die weitere Berechnung muss zuerst der wirkliche Restextrakt als Näherungswert bestimmt werden. Dies erfolgt anhand von Gl. 18 auf Basis der mit Gl. 3 ermittelten Stammwürze und, je nach Korrelationsmodell, dem mit Gl. 2 ermittelten scheinbaren Restextrakt.
Gl. 18
Durch das Einsetzen der Stammwürze und des wirklichen Restextrakts in Gl. 19 wird dann der Alkoholgehalt als Gewichtsanteil berechnet. Um den Volumensanteil zu erhalten, ist neben dem berechneten Ergebnis die durch die gewählte Korrellationfunktion ermittelte spezifische Dichte in Gl. 20 einzusetzen.
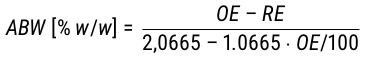
Gl. 19
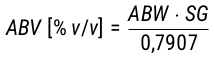
Gl. 20
Eine weitere Kennzahl, die aus den durchgeführten Messungen berechnet werden kann, ist der Vergärungsgrad. Dieser gibt an, zu welchem Anteil der ursprüngliche Extrakt während der Gärung konsumiert wurde. Für den scheinbaren Restextrakt wird der scheinbare Vergärungsgrad (Apparent Degree of Fermentation, ADF) gemäß Gl. 21 ermittelt. Der wirkliche Vergärungsgrad (Real Degree of Fermentation, RDF) ist nach Methode der American Society of Brewing Chemists (ASBC) durch Gl. 22 zu berechnen. Alternativ kann als Näherung der scheinbare Vergärungsgrad mit dem Ballingschen Umrechnungsaktor 0,81 multipliziert werden. (MEBAK, 2013, S. 131, 137 f.; Spedding, 2016, S. 116, 125; Speers, 2015)
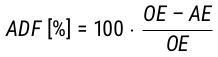
Gl. 21
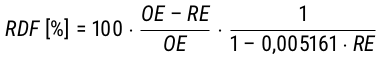
Gl. 22
Die auf den Etiketten von Bierflaschen abgedruckten Nährwertangaben sind zwar nur in Verbindung mit chemisch analytischen Verfahren feststellbar, lassen sich aber mithilfe von Gl. 23 und Gl. 24 für eine Schnellanalyse abschätzen (MEBAK, 2013, S. 161).
Gl. 23
Gl. 24
Eine Implementierung aller vorgestellten Berechnungen in der Form eines Refraktometer-Rechners ist über https://aschet.github.io/refractometer abrufbar.
Berechnungsbespiel
Bei einer mit einem Refraktometer gemessenen Stammwürze von Ri=12 und einem Restextrakt von Rf=6 ist bei einem Würze-Korrekturfaktor von WCF=1,04 mithilfe der linearen Terrill Formel (Gl. 9) der Alkoholgehalt des gemessenen Bieres zu berechnen. Unter Anwendung von Gl. 3, Gl. 9, Gl. 2, Gl. 18, Gl. 19 und Gl. 20 ergibt sich folgender Berechnungsweg:

Zusammenfassung
- Refraktometer messen auf Basis der Brechung des Lichts. Im Heimbrauumfeld eingesetzte Handgeräte sind zumeist mit einer Brix-Skala ausgestattet.
- Mit einem Refraktometer erfasste Messwerte müssen umgerechnet werden. Bei Messungen vor einer Gärung (Stammwürze) ist der Würze-Korrekturfaktor anzuwenden. Messungen nach einer Gärung unterliegen einer Verfälschung aufgrund des gebildeten Alkohols. Zur Korrektur wird ein Messwert mithilfe einer Korrelationsfunktion transformiert.
- Vor einer Messung sollte eine Kalibrierung und Justierung mit destilliertem Wasser bei Raumtemperatur erfolgen.
- Proben sind für die Messung aufzubereiten. Heiße Würze sollte in einem abgedeckten Container auf Raumtemperatur abgekühlt werden. Während oder nach einer Gärung entnommene Proben müssen bei der Messung frei von Schwebstoffen und Gasen sein. Enthaltenes CO2 lässt sich durch wiederholtes Schütteln entfernen. Enthaltene Hefe sedimentiert nach längerer Wartezeit.
- Zur Bestimmung des Alkoholgehalts ist eine Messung vor und eine nach einer Gärung durchzuführen. Mithilfe eines Refraktometer-Rechners lässt sich dann der Alkoholgehalt als Näherungswert berechnen: https://aschet.github.io/refractometer
Quellen
- A.KRÜSS Optronic GmbH. (2021). Wie funktioniert ein Refraktometer? Verfügbar 20. August 2021 unter https://www.kruess.com/campus/refraktometrie/wie-funktioniert-ein-refraktometer
- Bettner, R. E. & Meredith, W. O. S. (1969). Estimation of Malt Extract from Refractive Index of Wort. Proceedings. Annual meeting – American Society of Brewing Chemists, 27(1), 171–174. https://doi.org/10.1080/00960845.1969.12007114
- Bonham, L. K. (2001). The Use of Handheld Refractometers by Homebrewers. Zymurgy, 24(1), 43–46.
- Brew Science Homebrewing Blog. (2010). Refractometer Experiment. Verfügbar 20. August 2021 unter https://sciencebrewer.wordpress.com/2010/12/17/refractometer-experiment
- Brückelmeier, J. (2018). Bier Brauen: Grundlagen, Rohstoffe, Brauprozesse. Ulmer.
- DePalma, A. (2017). Refractometers: Secrects of Accurate Measurements. Verfügbar 7. August 2021 unter https://www.labmanager.com/product-focus/refractometers-secrets-of-accurate-measurement-3437
- Distillique. (2020). Incorrect Readings: Comparing Refractometer and SG Hydrometer Readings. Verfügbar 20. August 2021 unter https://distillique.co.za/Shop/blog/incorrect-readings-comparing-refractometer-and-sg-hydrometer-readings-n59
- Earl, B. (2015). Calibrating Sensors. Verfügbar 7. August 2021 unter https://learn.adafruit.com/calibrating-sensors
- Gamer, L. S. (1959). Adaptation of the Immersion Refractometer to the Determination of Extract and Alcohol in the Brewery. Proceedings. Annual meeting – American Society of Brewing Chemists, 17(1), 102–106. https://doi.org/10.1080/00960845.1959.12006866
- Gossett, J. M. (2012a). Contribution of Ethanol to Brix Measurements and Measurement of ABV Using Brix Refractometry. Verfügbar 1. August 2021 unter http://www.ithacoin.com/brewing/EtOH_to_Brix.htm
- Gossett, J. M. (2012b). Derivation and Explanation of the Brix-Based Calculator For Estimating ABV in Fermenting and Finished Beers. Verfügbar 1. August 2021 unter http://www.ithacoin.com/brewing/Derivation.htm
- Gossett, J. M. (2012c). A Refractometer-Based Method to Estimate ABV in Fermenting and Finished Beers. Verfügbar 1. August 2021 unter http://www.ithacoin.com/brewing/Overview.htm
- Kunze, W. (2004). Technology Brewing and Malting (3. Aufl.). VLB Berlin.
- MEBAK. (2013). Wort, Beer and Beer-based Beverages. Fritz Jacob.
- Narziss, L. & Back, W. (2009). Die Bierbrauerei: Die Technologie der Würzebereitung (8. Aufl., Bd. 2). WILEY-VCH.
- Novotný, P. (2017a). Počítáme: Nová korekce refraktometru. Verfügbar 1. August 2021 unter http://www.diversity.beer/2017/01/pocitame-nova-korekce-refraktometru.html
- Novotný, P. (2017b). Revisiting the Refractometer: Improved Fermentation Monitoring Through Refractometry. Zymurgy, 40(4), 49–54.
- Refractometers and final gravity. (2019). Verfügbar 29. August 2021 unter https://www.homebrewtalk.com/threads/refractometers-and-final-gravity.667581
- Roberts, F. J. & Stewart, T. J. (1950). Practical Applications of the Hand Refractometer to Brewing Operations. Proceedings. Annual meeting – American Society of Brewing Chemists, 8(1), 118–122. https://doi.org/10.1080/00960845.1950.12006580
- ŠAVEL, J., KOŠIN, P., BROŽ, A. & SIGLER, K. (2009). Convenient Monitoring Of Brewery Fermentation Course By Refractometry. Kvasny Prumysl, 55(4), 94–99. https://doi.org/10.18832/kp2009009
- Sean Terrill’s website issues. (2020). Verfügbar 29. August 2021 unter https://www.reddit.com/r/Homebrewing/comments/bs3af9/sean_terrills_website_issues
- Spedding, G. (2016). Alcohol and Its Measurement. Brewing Materials and Processes (S. 123–149). Elsevier. https://doi.org/10.1016/b978-0-12-799954-8.00007-1
- Speers, A. (2015). Brewing Calculations. Verfügbar 15. August 2021 unter https://chme.nmsu.edu/files/2017/03/FeatAug15.pdf
- Terrill, S. (2010a). Refractometer Estimates of Final Gravity. Verfügbar 4. März 2021 unter http://seanterrill.com/2010/06/11/refractometer-estimates-of-final-gravity/
- Terrill, S. (2010b). Toward a Better Refractometer Correlation. Verfügbar 28. Februar 2021 unter http://seanterrill.com/2010/07/20/toward-a-better-refractometer-correlation/
- Terrill, S. (2011). Refractometer FG Results. Verfügbar 18. Januar 2021 unter http://seanterrill.com/2011/04/07/refractometer-fg-results/
- Terrill, S. (2013). Using a Refractometer. Zymurgy, 36(4), 49–53.
- Troester, K. (2012). Don’t Trust Your Refractometer Blindly. Verfügbar 1. August 2021 unter http://braukaiser.com/blog/blog/2012/03/23/dont-trust-your-refractometer-blindly/
- Wolf, S. (2015). Gemeinschaftsexperiment Spindel-Refraktometer Korrelation. Verfügbar 21. August 2021 unter https://maischemalzundmehr.de/index.php?inhaltmitte=exprefraktometer









Blog Comments
Oliver Weiss
3. Januar 2024 at 14:06
Hallo Herr Ascher,
das ist eine ganz wunderbare Arbeit, die sie hier abgeliefert haben. Mit das Beste, was ich je über diesen Themenkreis gelesen habe.
Viele Grüße
Oli Weiss
P.S.: Sollten Sie den Gebhard Sauseng(Anton Paar) sehen, dann richten Sie doch bitte beste Grüße von mir aus.
Thomas Ascher
4. Februar 2024 at 19:22
Besten Dank für das Kompliment! Die Grüße leite ich gerne weiter.
Patrick Steiner
19. September 2024 at 9:04
Guten Tag Herr Ascher,
Sehr schön dokumentiert und erklärt.
Zu Gleichung 2: Müsste da nicht
AE [g/100g]=… anstatt °P [g/100g]=… stehen?
Schöne Grüsse
Patrick Steiner
Thomas Ascher
6. Oktober 2024 at 18:51
Hallo Patrick,
freut mich, positives Feedback zu meinem Artikel zu bekommen. Ja, ich stimme zu, im Kontext des Artikels und des Rechenbeispiels wäre es besser, wenn bei Gleichung 1 und 2 AE anstatt °P (OE) stehen würde. Nebenbei fällt mir noch auf, dass bei Gleichung 1 im Nenner das Gradzeichen bei P fehlt. Beide Gleichungen habe ich aus „Alcohol and Its Measurement“ von Spedding ab Seite 140 entnommen und um die Einheit [g/100g] ergänzt, wobei die Gleichung 2 als „Plato Extract = …“ formuliert war. Nachdem aber die Gleichung 1 im Prinzip die Umkehrfunktion von Gleichung 2 ist, habe ich deren Schreibweise übernommen. Interessanterweise wird in derselben Quelle etwas später als Alternative die Goldiner Gleichung als „AE = -202,414 SG^2 + 662,649 SG – 460,234“ angegeben. Nachdem alle diese Gleichungen meines Wissens nach das Extraktgehalt zu Dichte Verhältnis auf Basis der Plato Tabellen beschreiben, wäre rein formal „OE = …“ wohl korrekt.
Beste Grüße
Thomas